文/阿樹 《震識:那些你想知道的震事》副總編輯
建議閱讀本文前,先稍微了解地震規模的一二事,或先讀過這篇:
地震規模計算方法的演進歷史,也記載了我們對地震與斷層看法的演變
記得我以前學到的知識是「地震規模只有一個」,我也一直都相信這件事。不過在接觸實務的地震定位和規模計算後,卻發現一件有趣的事,那就是「原來計算上的規模值可能不止一個!」由於當初在求地震規模時,使用的參數是儀器的最大振幅值,但因為每一個地震測站所在地的地質特性不一,而造成計算結果不同。而我們對地底下的地質變化了解的尺度其實頗為粗糙,所以要把結果不同的誤差完全修正,幾乎是不可能的。
這問題芮克特也是有想過的,但規模是用來描述地震本身的大小,定義上本來也只能有一個值,所以求出震源位置、計算規模時,實務上會把各地測站求得的規模值作平均,這也是為什麼地震規模只會到小數點後一位,因為精度是有限的。以現今的地震站密度以及我們對地下構造的了解,大多時候如果增加了數個測站後,還需要修正的地震規模值,大概頂多只差個0.1、0.2左右,所以下次你看到事後有修正規模值或是不同單位的結果不同,也不需要太意外了!
芮氏規模的發展和修改歷史
在本站的(課本沒教的芮氏規模)一文,有提到了最早設計規模的人是芮克特和古騰堡,好像我們都忘了後面那位厲害的科學家,連名字都忘了放上去,但他其實也做了某程度的貢獻。他和芮克特發現芮氏規模會有「飽合」的問題,簡單來說就是明明規模應該是遠大於6.0很多的地震,用芮氏規模的計算方式,怎麼樣都只有6.0~6.5不等。
(以下為對白部分純屬想像,不代表真實故事)
「這其中一定是有什麼誤會!」古騰堡表示。
「這的確很麻煩,其實扣除那些大地震,我們的方法還是很好用啊!」芮克特不想改變這套計算系統。
「不然,我們調整一下做法好了,看能不能調整公式,或是把不同類型的波分別處理(見文末註1)?」
所以後來古騰堡又發明了不同規模的計算方式,包括只利用實體波(P波、S波)的「體波規模」mb,還有另一種專門可以用在大地震上的「表面波規模」Ms,正好銜接上原先規模的計算上限。所以最後我們現今常用的芮氏規模之所以可以算出大於規模7的值,也是因為後來古騰堡改良了原先規模太大會達飽和的問題。而與其說我們的規模是用芮氏規模,不如說它是「近震規模」,其標示ML的下標L,本來就是指local magnitude的意思!
但是,其實問題還是沒有完全解決呢!
「飽和」的根本原因
對於超大型等級的大地震(規模8、9以上的地震,像2011年東日本大地震、2004蘇門答臘地震)的「近震規模」,即使有了表面波規模的加持,但終究還是出現「飽和」的情況,這其實反映了我們看待地震的問題。
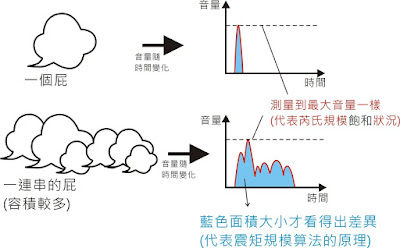
以現今的科學角度來看,近震規模的計算方式其實有盲點。大多時候,斷層錯動釋放能量引發地震時,往往會發生在很快的一瞬間,但是斷層的尺度一旦變得很大時,那一瞬間有可能會變得相對久得多。用一個稍微不衛生但相對好懂的例子:我們用不同的工具來測量「誰放的屁較大」時,便會有不同的結果。
我們先試想兩種放屁的情境:
1、在1秒之內放了一個響屁。
2、花10秒時間緩慢的放了一連串的屁,最大音量和前者接近。
如果我們僅只測量屁聲的音量來評斷屁的大小,第2種情況產生的屁量「容積」雖較大,但因為屁聲的分貝數相近,所以會發生低估屁量的情況。
所以,近震規模之所以飽和,代表的就是它沒辦法正確且完整的測量斷層錯動引發地震所釋放的能量。芮氏規模的計算方式僅計得了最大規模,但斷層的錯動時間可能很快,也很可能很慢,在數日之前的一篇「潛移斷層」的介紹文中,提到了斷層錯動甚至可以慢到不會發生地震。
如果所有的斷層面只是在一瞬間(數秒鐘左右)滑動,那麼用地震波最大振幅來估算,應該不會有太大問題,可這種情況多半只發生在規模較小的地震。當地震大到8.0以上,滑動就有可能花上很長的時間,近代最極致的例子,就是2004年蘇門答臘Mw=9.3的地震,整條斷層錯動的時間花了將近10分鐘。至於最近一次超過規模9的311東日本大地震(Mw=9.1),斷層錯動的時間也超過3分鐘,這已經算是非常快的滑動速度了!
 |
| 2011年東日本大地震時,斷層破裂與錯動情況,斜向長方形範圍代表斷層的分布(麻煩請發揮想像力,它是一個右高左低、在地底下的斜面),等值線和彩色代表它的滑動量分布,黑色箭頭代表滑動方向。紅色星號代表震央,紫紅色圓圈代表餘震的分布位置。圖取自Lee, 2011. [2]。 |
金森博雄教授發明的「震矩規模」
要說明解決地震規模的新發明「震矩規模」,就不得不提它的創立者,就是加州理工學院的金森博雄教授(Hiroo Kanamori,金森教授同是本站催生者馬國鳳教授的指導教授,對阿樹來說是「老師的老師」輩了XD)。金森博雄用了我們國中都稍微接觸過的物理意義來解決這個問題:斷層做的「功」,就是地震釋放的能量。
而金森博雄在計算地震能量時,便創立了一個新單位:「地震矩」,利用斷層的滑動量、斷層的面積和斷層面的特性(剛性係數)這三個參數算出來。由這三個參數算出的「地震矩」,一般會以Mo表示,它雖然像是「力矩」的概念,但也相當於地震釋放的能量。(見文末註2)
這三個參數或是其計算結果的「地震矩」要怎麼得到呢?大地震後的地表變形,讓我們知道斷層的長度、錯動的程度和地表變形的範圍,而大地震過後的餘震也能告訴我們地底下斷層面可能的分布情形,再加上一些地震波形藏的資訊,這些都能幫我們估出地震矩。但受限於科技,早期的地震儀就像是比較低階的錄音機,能記下的震波有限,直至寬頻地震儀的問世(1988年),我們「錄製」地震的波形能力大幅提升,現在也能藉由地震波直接估算出震矩,只要有「完整的地震波形」,就能算出地震的總能量。
不過Mo的值既然是代表地震的總能量,那麼可想而知其值非常大,不過這個問題芮克特和古騰堡早就已經解決了,用對數(取log值)的方式來建立公式就可以讓它的標示單純化。說到這,阿樹也不禁感慨,原來當初念書時學的微積分、工程數學真的是有用處的啊!(笑)
 |
| 地震規模算法的具像化比喻差異,不代表真實的計算方式。因為計算地震矩時會用上完整的地震波形,等於把能量釋放隨時間的變化也都考量進去,更能反映真實能量情況。 |
不同規模之間的「差異問題」
用震矩規模的方式來計算並描述地震,既不會有飽合,小地震也都能套用,可以說是「更先進」的計算方法。但也因為它是完整的計算能量,和其它的規模計算方法間的轉換就不太好作換算,因為不同的規模的計算方法已經不是在算同樣的參數了,自然無法容易轉換。在震矩規模開始發展以前所使用的那些近震規模,就難以再轉換回來,這樣在統計過去的地震規模時,就會有單位使用不一致的情形,所以其實蠻多地區的監測單位仍使用近震(芮氏)規模來描述地震。
或許有人會認為「既然有個更先進的方式,為什麼還要用比較舊而且有缺點的方法?」不過就像前面提到的,以長期地震紀錄來看,兩者並行或許是更好的方式,當然我們現在也已經在做了,只是中央氣象局公告的資料還是以芮氏規模為主。
附帶一提,有些時候,震矩規模和芮氏規模計算結果的「差異」,也透露了一些科學訊息。有一種「慢地震」,顧名思義就是滑移速度較慢的地震,如果它的斷層類型是正斷層或逆斷層,又發生在海底時,斷層錯動造成的大規模海水波動,有可能引發大海嘯。從前面提到的計算原理來看,正因為慢地震的滑移的速度較慢,往往會讓儀器收到的振幅較小,芮氏規模因而較為低估,因此當我們發現兩者的差異很大,且又發生在海底時,就要特別當心這現象。
這樣看來,或許地震矩規模有它「先進」的地方,但並不代表芮氏規模就「不好」,畢竟芮克特和古騰堡將地震的能量計算回歸地震波形,並用對數的方式做處理表示,已經是一個劃時代的做法。而金森博雄教授再進一步的量化方式,讓我們更了解地震發生過程和能量釋放的方式,又讓地震科學再更上一層樓。我想對人們來說,只要清楚知道自己用的是什麼單位即可,就像計算容積時用「公升」還是「加侖」都行,只要講清楚、說明白,方是科學之道!
註2:如果忘記「功」是什麼,可以重新翻開國中自然課本,裡面有個W=F x S的公式,即「功」=「作用力」乘上「作用的距離」,譬如提重物走一層樓,作用距離就是一層樓的高度。不過,斷層是個塊體相對運動,另一個公式可能更能說明斷層上的情況,那就是力矩的公式:L=F x D,即「力矩」=「力」乘上「力臂」。
參考資料:


沒有留言:
張貼留言